菱形的面积公式是什么呢?
菱形的面积公式:
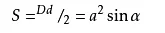
菱形面积公式就是由三角形面积公式得来的。菱形面积=两个三角形面积的和。
对角线乘积的一半,即S=(两对角线相乘)X1/2(只要是对角线互相垂直的四边形都可用,如正方形,菱形,记为:二分之一对角线相乘)。
判断:
在同一平面内,
一组邻边相等的平行四边形是菱形;
对角线互相垂直的平行四边形是菱形;
四条边均相等的四边形是菱形;
对角线互相垂直平分的四边形;
两条对角线分别平分每组对角的四边形;
有一对角线平分一个内角的平行四边形;
菱形是在平行四边形的前提下定义的,首先它是平行四边形,而且是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而增加了一些特殊的性质和判定 *** 。
菱形的一条对角线必须与x轴平行,另一条对角线与y轴平行。不满足此条件的几何学菱形在计算机图形学上被视作一般四边形。
菱形的面积公式是怎么样的呢?
菱形的面积公式有以下几种:
1、菱形面积公式就是由三角形面积公式得来的。菱形面积=两个三角形面积的和;
2、S=1/2(对角线×对角线)(即菱形的面积也等于对角线乘积的一半) ;
3、底×高=菱形面积;
4、 设菱形的边长为a,一个夹角为θ,则面积公式是:S=a^2·sinθ。
菱形的定义:一组邻边相等的平行四边行是菱形。

菱形的性质:
1、四条边都相等;
2、对角线互相垂直平分(不一定相等);
3、一条对角线分别平分一组对角。
它具有平行四边形的所有性质。
菱形的判断定理:
1、一组邻边相等的平行四边形是菱形;
2、四边相等的四边形是菱形;
3、对角线互相垂直的平行四边形是菱形;
4·、对角线互相垂直平分的四边形是菱形。
下面分享相关内容的知识扩展:
如何证明菱形的面积等于其对角线乘积的一半
由菱形的定义可知,菱形被对角线分成4个全等的直角三角形,并且相交于中点。
那么可以把菱形看做两个对着的全等三角形,以其中一条对角线划分。假设为对角线a和对角线b,一个三角形的面积是:对角线a×(对角线b÷2)÷2 ;那么两个这样的三角形就是菱形的面积了。也就是:
对角线a×(对角线b÷2)÷2×2=对角线a×(对角线b÷2)=对角线a×对角线b÷2,由此可知菱形的面积就是对角线乘积的一半。
扩展资料
通过证明菱形的面积等于对角线乘积的一半,可以得到菱形的性质有:
1、菱形具有平行四边形的一切性质;
2、菱形的四条边都相等;
3、菱形的对角线互相垂直平分且平分每一组对角;
4、菱形是轴对称图形,对称轴有2条,即两条对角线所在直线;
5、菱形是中心对称图形;
菱形是在平行四边形的前提下定义的,首先它是平行四边形,而且是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而增加了一些特殊的性质和判定 *** 。
菱形的一条对角线必须与x轴平行,另一条对角线与y轴平行。不满足此条件的几何学菱形在计算机图形学上被视作一般四边形。
参考资料百度百科-菱形
关于菱形的所有公式(面积 周长 对角线 角度 边长)的急需啊!好的话给30分啊!!!
1菱形面积公式就是由三角形面积公式得来的。菱形面积=两个三角形面积的和 2.对角线乘积的一半,即S=(a×b)÷2(只要是对角线互相垂直的四边形都可用)。 3.S菱形=底*高(跟平行四边形面积公式一样,菱形是特殊的平行四边形)。 4.面积公式是:a-边长 α-夹角 D-长对角线长 d-短对角线长 S=Dd/2 =a2sinα 。 5.边长的平方减去对角线差一半的平方。请问菱形的面积计算公式?请用最简单的道理详细说明好吗谢谢 另:正方形本身就是特殊的菱形,这句话怎
请问菱形的面积计算公式?请用最简单的道理详细说明好吗谢谢 另:正方形本身就是特殊的菱形,这句话怎么讲?如果它是特殊的菱形,正方形的面积=底×高,菱形的面积同样也应该=底×高,对吗?请纠正谢谢 另外你能给我画个图吗?是不是只要算出个三角形的面具就可以知道菱形的面积谢谢菱形的面积确实可以用底×高去算,只不过原因是菱形是特殊的平行四边形,平行四边形可以用底×高,所以菱形也可以,而不是因为正方形能用底×高推出菱形可以用底×高,因为特殊情况具有的性质一般情况不一定具有。
菱形的高是由一个顶点向对边引垂线(不是该顶点所在的边),用这条边和所对应的高相乘即可的面积。
另外菱形面积可以又对角线乘积的一半得到。原因是菱形的对角线互相垂直。
连接菱形的一条对角线,可以将菱形分成两个全等的三角形,算出一个的面积乘2就可以了。







