分数乘法是数学中一个重要的概念,它是指两个分数相乘的运算。在实际应用中,分数乘法可以用于计算面积、体积、速度等问题。分数乘法的意义不仅仅是计算,它还涉及到数学思维和乘法本质的探究。本文将从多个角度探究分数乘法的意义。
分数乘法的定义
分数乘法是指两个分数相乘的运算,可以表示为:$\frac{a}{b} \times \frac{c}{d} = \frac{ac}{bd}$。其中,$\frac{a}{b}$和$\frac{c}{d}$分别表示两个分数,$\frac{ac}{bd}$表示它们的积。这个定义告诉我们,分数乘法的本质是将两个分数的分子和分母分别相乘,并将结果约分得到积。
分数乘法的几何意义
分数乘法的几何意义是指将分数看作长度、面积或体积的比例。例如,$\frac{3}{4}$可以表示一个长方形的宽度比长度为3:4。$\frac{3}{4} \times \frac{2}{5}$表示什么意思呢?它可以表示一个长方形的宽度比长度为3:4,再将宽度缩小到$\frac{2}{5}$,得到一个新的长方形。这个新长方形的面积就是$\frac{3}{4} \times \frac{2}{5}$。
分数乘法的实际应用
分数乘法在实际应用中非常重要,例如计算面积、体积、速度等问题。例如,一个长方形的宽度为$\frac{3}{4}$米,长度为$\frac{2}{5}$米,那么它的面积就是$\frac{3}{4} \times \frac{2}{5} = \frac{3}{10}$平方米。再例如,一个人以每小时$\frac{3}{4}$米的速度行走,走了$\frac{2}{5}$小时,那么他走的距离就是$\frac{3}{4} \times \frac{2}{5} = \frac{3}{10}$米。
分数乘法的算术意义
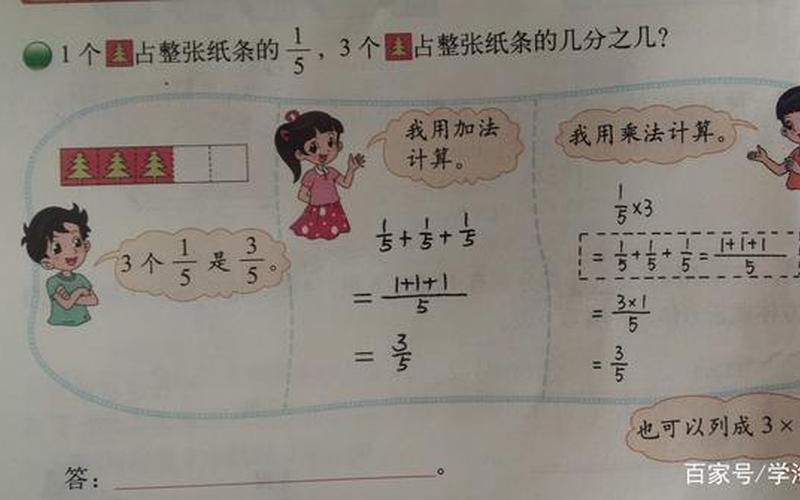
分数乘法的算术意义是指将乘法看作加法的重复。例如,$\frac{3}{4} \times 2$可以看作$\frac{3}{4} + \frac{3}{4}$,也就是将$\frac{3}{4}$加上自己一次,再加上自己一次。这样,我们就可以将分数乘法转化为分数加法,从而更容易进行计算。
分数乘法的数学思维
分数乘法的数学思维是指通过分数乘法的运算,培养学生的数学思维能力。例如,分数乘法可以帮助学生理解分数的大小关系,掌握分数的约分和通分 *** ,以及培养学生的逻辑思维和推理能力。
分数乘法的本质意义
分数乘法的本质意义是指探究乘法的本质特征。乘法的本质特征是将两个数相乘得到一个新的数,这个新的数是原来两个数的某种组合。分数乘法是乘法的一个特例,它的本质特征是将两个分数的分子和分母分别相乘,并将结果约分得到积。
分数乘法与分数除法的关系
分数乘法和分数除法是数学中两个重要的概念,它们之间存在着密切的关系。例如,$\frac{3}{4} \div \frac{2}{5}$可以转化为$\frac{3}{4} \times \frac{5}{2}$,也就是将被除数和除数互换,再将除法转化为乘法。这个例子告诉我们,分数乘法和分数除法之间存在着互逆的关系。
分数乘法是数学中一个重要的概念,它不仅仅是用来计算的工具,还涉及到几何意义、实际应用、算术意义、数学思维和乘法本质的探究。通过深入理解分数乘法的意义,可以更好地掌握分数乘法的运算 *** ,提高数学思维能力,以及更好地理解数学中其他相关概念。







