平均化探索是一种数据分析 *** ,它的核心思想是通过平均化的方式,探究数据的规律和趋势。平均化探索的目的是为了更好地理解数据,从而做出更准确的预测和决策。在平均化探索中,平均数是一个非常重要的指标,它可以帮助我们快速了解数据的中心趋势和分布情况。万福小编龙啊啊会对平均化探索进行详细的分享。
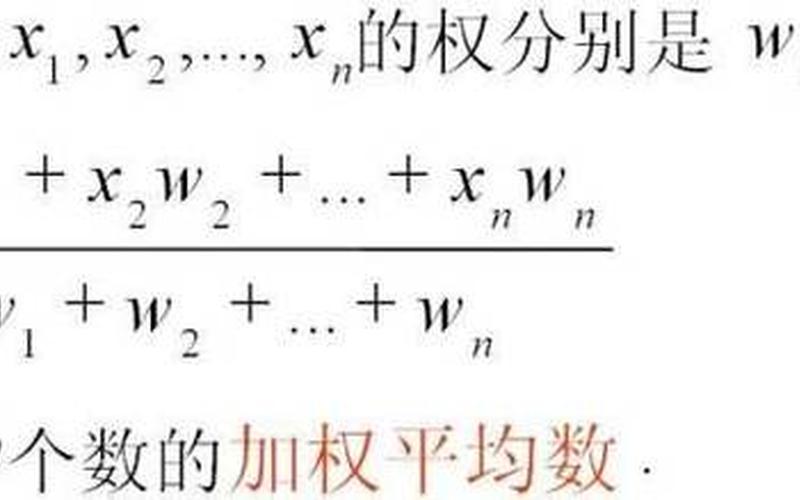
平均数的定义和计算 ***
平均数是一组数据的总和除以数据的个数,它可以反映这组数据的中心趋势。在平均化探索中,我们常常使用算术平均数来表示一组数据的平均值。算术平均数的计算 *** 非常简单,只需要把这组数据的总和除以数据的个数即可。例如,对于数据集{1,2,3,4,5},它们的平均数为(1+2+3+4+5)/5=3。
平均数的应用场景
平均数在数据分析中有很广泛的应用,例如在统计学、经济学、物理学等领域都有使用。在商业领域中,平均数可以用来计算销售额、利润、成本等指标的平均值,从而帮助企业了解自己的经营情况。在医学领域中,平均数可以用来计算患者的平均年龄、身高、体重等指标,从而帮助医生更好地了解患者的健康状况。
平均数的优缺点
平均数作为一种衡量数据中心趋势的指标,具有以下优点:1.易于计算,只需要简单的加减乘除即可。2.能够反映数据的中心趋势,对于一组数据的总体情况有较好的概括作用。平均数也存在一些缺点:1.容易受到极端值的影响,如果数据中存在极端值,平均数可能会失去代表性。2.不能反映数据的分布情况,对于数据的离散程度无法进行有效的描述。
平均数与其他指标的比较
除了平均数,还有中位数、众数等指标可以用来衡量数据的中心趋势。中位数是将一组数据按照大小顺序排列后,位于中间位置的数值,它不受极端值的影响,能够反映数据的中心位置。众数是一组数据中出现次数最多的数值,它可以反映数据的集中程度。与平均数相比,中位数和众数更适合用来描述非正态分布的数据。
如何选择合适的平均数
在实际应用中,我们需要根据数据的特点和分布情况来选择合适的平均数。如果数据呈正态分布,那么算术平均数是一个比较好的选择;如果数据存在极端值,那么可以考虑使用中位数等鲁棒性更强的指标。还可以使用加权平均数、几何平均数等不同类型的平均数来适应不同的数据场景。
平均数的局限性及解决方案
平均数作为一种常用的数据分析指标,虽然具有一定的优点,但也存在一些局限性。例如,平均数容易受到极端值的影响,不能反映数据的分布情况等。为了克服这些局限性,可以采用一些解决方案,例如:1.使用中位数等鲁棒性更强的指标;2.使用加权平均数等不同类型的平均数;3.结合其他指标进行综合分析等。通过这些 *** ,可以更好地利用平均数这一指标,探究数据的规律和趋势。
平均化探索在实际应用中的案例
平均化探索在实际应用中有很多成功的案例。例如,在金融领域中,平均化探索可以用来分析股票市场的走势,预测未来的股价变化。在医疗领域中,平均化探索可以用来分析患者的病情、药物的疗效等,从而帮助医生做出更准确的诊断和治疗方案。在人力资源管理中,平均化探索可以用来分析员工的绩效、薪酬等,从而帮助企业做出更合理的人力资源决策。
平均化探索是一种非常重要的数据分析 *** ,它可以帮助我们更好地理解数据的规律和趋势。在平均化探索中,平均数是一个非常重要的指标,它可以反映数据的中心趋势。平均数也存在一些局限性,需要结合其他指标进行综合分析。通过合理地选择平均数和采用一些解决方案,可以更好地利用平均化探索这一 *** ,为实际应用提供更准确、更有价值的数据分析结果。







