cotx等于这个吗
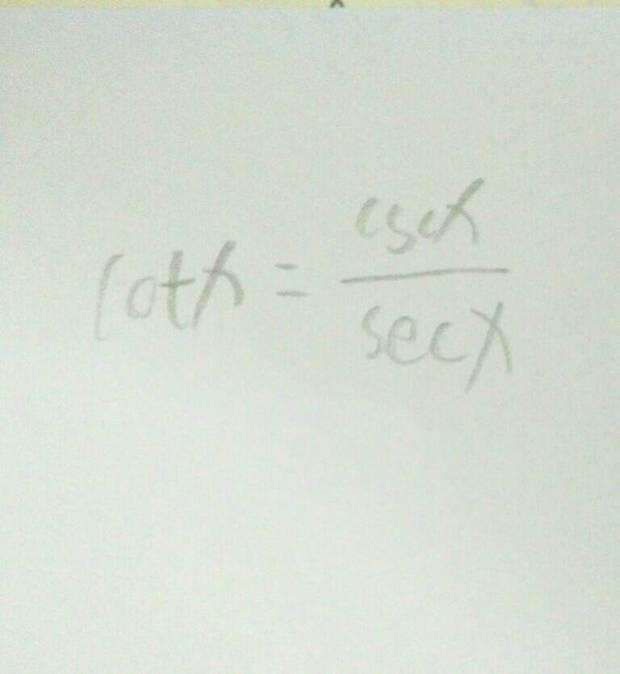
cot是余切,也就是1/tan也就是cos/sin csc是余割=1/sin,sec是正割=1/cos,csc/sec=cos/sin就是余切,所以这个等式是成立的。将一个角放入直角坐标系du中,使角的始边与X轴的非负半轴重合,在角的终边上找一点A(x,y)过A做X轴的垂线,则r=(x^2+y^2)^(1/2),cotθ=x/y,余切无更大最小值。
诱导公式:cot(kπ+α)=cotα、cot(π/2-α)=tanα、cot(π/2+α)=-tanα、cot(-α)=-cotα、cot(π+α)=cotα、cot(π-α)=-cotα。
特殊角:cot30°= √3、cot45°=1、cot60°=(√3)/3、cot90°=0。
扩展资料:在直角三角形中,某锐角的相邻直角边和相对直角边的比,叫做该锐角的余切。余切与正切互为倒数,用“cot+角度”表示。余切函数的图象由一些隔离的分支组成。余切函数是无界函数,可取一切实数值,也是奇函数和周期函数,其最小正周期是π。参考资料来源:百度百科-余切
cotx等于什么 cotx等于啥呢

1、cotX=1/tanX=cosX/sinX。
2、在坐标轴里,cotx=x/y。对于任意一个实数x,都对应着唯一的角(弧度制中等于这个实数),而这个角又对应着唯一确定的余切值cotx与它对应,按照这个对应法则建立的函数称为余切函数。
下面分享相关内容的知识扩展:
arccotx的导数是多少
f(x)=arccotx,则导数f′(x)=-1/(1+x2).
证明如下:
设arccotx=y,则
coty=x
两边求导,得
(-csc2y)·y′=1,
即y′=-1/csc2y=-1/(1+cot2y),
因此,
y′=f′(x)=-1/(1+x2)。
一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。
扩展资料:
常见导数公式
y=f(x)=c (c为常数),则f'(x)=0
f(x)=x^n (n不等于0),f'(x)=nx^(n-1) (x^n表示x的n次方)
f(x)=sinx,f'(x)=cosx
f(x)=cosx,f'(x)=-sinx
导数运算法则:
(f(x)+/-g(x))'=f'(x)+/- g'(x)
(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)
(g(x)/f(x))'=(f(x)'g(x)-g(x)f'(x))/(f(x))^2
求y=cotx的定义域,是x≠kπ还是x≠kπ/2
cotx=1/tanx 所以必须保证tanx有意义 且不等于0所以是x≠kπ且x≠kπ+π/2
余切函数y= cotx有什么样的性质?
余切函数y=cotx的性质
1、周期性:是周期函数,周期为kπ(k∈Z且k≠0),最小正周期T=π;
2、单调性:在每一个开区间(kπ,(k+1)π),k∈Z上都是减函数,在整个定义域上不具有单调性;
3、奇偶性:奇函数,可由诱导公式cot(-x)=-cotx推出图像关于原点对称,实际上所有的零点都是它的对称中心。
余切函数
在y=cotx中,以x的任一使cotx有意义的值与它对应的y值作为(x,y),在直角坐标系中,作出y=cotx的图形叫余切函数图象。也叫余切曲线。它是由相互平行的x=kπ(k∈Z)直线隔开的无穷多支曲线所组成的。
形式是f(x)=cotx,在平面直角坐标系中,函数y=cotx的图像叫做余切曲线。它是由相互平行的x=kπ(k∈Z)直线隔开的无穷多支曲线所组成的。







