怎么样理解静电场中的高斯定理
大学物理静电场高斯定理意思是:通过闭合曲面的电通量只与闭合面内的自由电荷代数和成正比。
这个定理反应了静电场是有源的,自由电荷就是产生磁场的源。
也反映了电场线是不闭合的,它从正电荷出发,到负电荷截止。
要注意的是,虽然电通量只取决于闭合曲面内部的自由电荷,但是闭合面上的场强,是内部电荷与外部电荷共同决定的。 在外部放上不同的电荷,闭合面上的场强就会发生不同的变化,但是该闭合面的电通量不变,只要内部电荷不变。
高斯定理用来求对纯分布的电荷产生的电场强度,十分方便。
你可以和磁场的高斯定理联系起来理解。磁场线是闭合的,所以必然是无源的,因为他的闭合,所以,磁场线穿进闭合曲面,必然会再传出来,磁通量对闭合曲面来说,永远是0
有关静电场中高斯定理
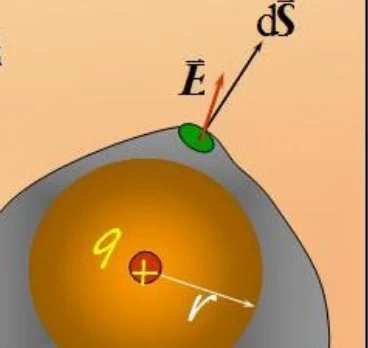
首先高斯面上的场强受外界影响,有一均匀实心带电球,算球内场强(该点不在壳上)时
利用高斯定理计算时,为什么不考虑高斯面外的电荷?
高斯定理计算的场强是单独高斯面内电荷形成的场强,
还是该面上的合场强?
计算的是该面上的合场强。
之所以不考虑面外的电荷是因为高斯面上电场的通量只取决于高斯面包围的电荷,这是由经电场的有源性决定的。
下面分享相关内容的知识扩展:
高斯定理数学公式是什么?
高斯定理数学公式是:∮F·dS=∫(▽·F)dV。
在静电学中,表明在闭合曲面内的电荷之和与产生的电场在该闭合曲面上的电通量积分之间的关系。 高斯定律(Gauss' law)表明在闭合曲面内的电荷分布与产生的电场之间的关系。
高斯定律在静电场情况下类比于应用在磁场学的安培定律,而二者都被集中在麦克斯韦方程组中。因为数学上的相似性,高斯定律也可以应用于其它由平方反比律决定的物理量,例如引力或者辐照度。
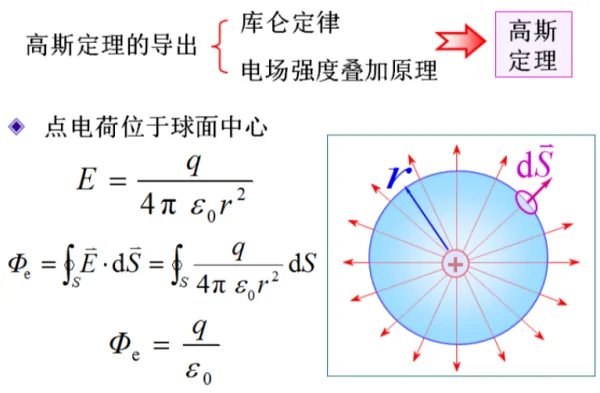
静电场与磁场
两者有着本质上的区别。在静电场中,由于自然界中存在着独立的电荷,所以电场线有起点和终点,只要闭合面内有净余的正(或负)电荷,穿过闭合面的电通量就不等于零,即静电场是有源场。
而在磁场中,由于自然界中没有磁单极子存在,N极和S极是不能分离的,磁感线都是无头无尾的闭合线,所以通过任何闭合面的磁通量必等于零。
平行板电容器的场强公式的推导,用高斯定理,要详细!
平板电容器由两个彼此靠得很近的平行极板(设为a和b)所组成,两极板的面积均为s,设两极板分别带有+q,-q的电荷。每块极板的电荷密度为σ=q/s,除去极板的边缘效应,板间的电场看成是均匀电场,所以由高斯定理得两板间场强为e=σ/ε。
由s/d即平板电容公式可得出c=s/4πkd。
高斯定理,静电场的基本方程之一,它给出了电场强度在任意封闭曲面上的面积分和包围在封闭曲面内的总电量之间的关系。
高斯定理定义:通过任意闭合曲面的电通量等于该闭合曲面所包围的所有电荷量的代数和与电常数之比。
电场强度公式:在匀强电场中,e=u/d
若知道一电荷受力大小可用,则e=f/q点电荷形成的电场得:e=kq/r^2(k为一常数,q为此电荷的电量,r为到此电荷的距离)可得出:随r的增大,点电荷形成的场强逐渐减小,不与r成正比,只与r^2成正比。
高斯定理 说明了静电场的哪些性质 电力线不是闭合曲线 库仑力是保守力
静电场的高斯定理说明静电场是有源场,电荷就是电场的源。
高斯定理是静电学中的一个重要定理 , 它反映了静电场的一个基本性质 ,即静电场是有源场 , 其源即是电荷。可表述为 : 在静电场中 , 通过任意闭合曲面的电通量 , 等于该闭合曲面所包围的电荷的代数和的 1/(电介质常数)倍,与闭合曲面外的电荷无关。
高斯定理是用来求场强 E 分布,定理中,S 是任意曲面,由于数学水平的限制,要由高斯定理计算出 E,则对由场的分布有一定的要求,即电荷分布具有严格的对称性。若电荷分布不对称性即不是均匀的 , 引起电场分布不对称,不能从高斯定理求空间场强分布 , 高斯定理当然仍是成立的。
扩展资料:
由于电荷分布的对称性导致场强分布的对称性 , 场强分布的对称性应包括大小和方向两个方面。
典型情况有三种 :
1、球对称性 , 如点电荷 , 均匀带电球面或球体等 ;
2、轴对称性 , 如无限长均匀带电直线 , 无限长均匀带电圆柱或圆柱面 ,无限长均匀带电同轴圆柱面
3、面对称性 , 如均匀带电无限大平面或平板 , 或者若干均匀带电无限大平行平面。
参考资料来源:百度百科-高斯定理







