什么是弧正切函数?
弧正切函数是一种三角函数,通常表示为arctan(x),它的定义域是实数集,值域是(-π/2, π/2)。弧正切函数的反函数是正切函数,也就是tan(x)。在数学中,弧正切函数通常用于计算一个角度的正切值,或者计算一个直角三角形的角度。
弧正切函数的图像
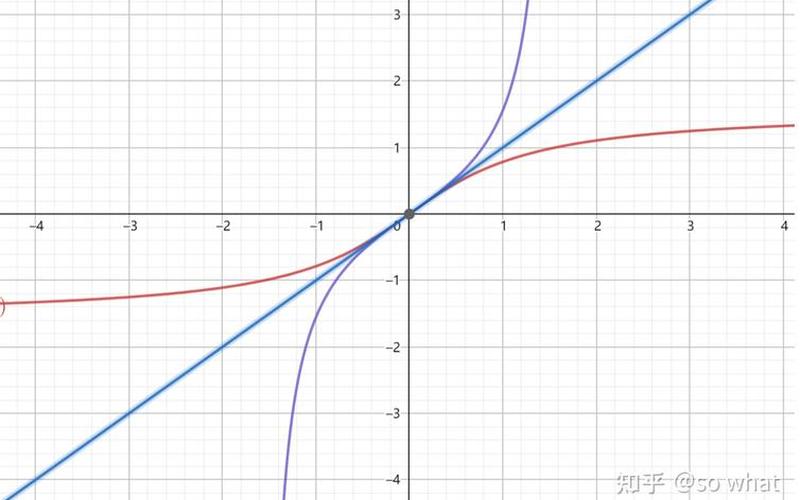
弧正切函数的图像是一条光滑的曲线,它的斜率在x轴两端趋近于无穷大,在中间部分斜率逐渐减小。这条曲线在x=0处有一个垂直渐近线,也就是说,当x趋近于0时,弧正切函数的值趋近于无穷大或者无穷小。
弧正切函数的性质
弧正切函数有许多有趣的性质。它是一个奇函数,也就是说,arctan(-x)=-arctan(x)。它是一个严格单调递增函数,在定义域内没有局部极值点。它是一个连续函数,在定义域内没有间断点。
弧正切函数的应用
弧正切函数在数学中有许多应用。它可以用于计算一个角度的正切值,或者计算一个直角三角形的角度。它还可以用于解决一些复杂的微积分问题,比如求解一些积分或者微分方程。
弧正切函数的变换
弧正切函数可以通过一些简单的变换来得到其他的函数。例如,通过对arctan(x)进行平移和缩放,可以得到一些新的函数,比如arctan(ax+b)。这些新的函数可以用于解决一些特殊的问题,比如求解一些非线性方程组。
弧正切函数的近似值
弧正切函数的值可以通过一些近似 *** 来计算。例如,可以使用泰勒级数来计算arctan(x)的近似值,或者使用牛顿迭代法来求解arctan(x)的精确值。这些 *** 在实际计算中非常有用,可以大大提高计算效率。
弧正切函数的应用实例
弧正切函数在实际应用中有许多实例。例如,在机器学习中,它可以用于计算神经 *** 的激活函数,或者用于优化算法的目标函数。在物理学中,它可以用于计算一些复杂的物理问题,比如计算电路的电流和电压。
弧正切函数的未来发展
弧正切函数在未来的发展中将继续发挥重要作用。随着计算机技术的不断发展,弧正切函数的计算 *** 也将不断改进,从而提高计算效率和精度。随着人工智能技术的不断发展,弧正切函数也将被广泛应用于各种智能系统中,从而实现更加智能化的计算和决策。







