指数与指数幂的运算怎么看
同底数幂的乘法:底数不变,指数相加同底数幂的除法:底数不变,指数相减幂的乘方:底数不变,指数相乘积的乘方:等于各因数分别乘方的积商的乘方(分式乘方):分子分母分别乘方,指数不变指数与指数幂的运算技巧
同底数幂的乘法:底数不变,指数相加同底数幂的除法:底数不变,指数相减
幂的乘方:底数不变,指数相乘
积的乘方:等于各因数分别乘方的积
商的乘方(分式乘方):分子分母分别乘方,指数不变
下面分享相关内容的知识扩展:
指数函数相加?
1.对于指数函数相加减,只好提取公因式,没有类似指数幂的运算法则.
2.对于对数函数相加减,则可以利用对数的运算法则进行计算,但要注意定义域.
指数运算公式大全法则及公式
指数运算公式大全法则及公式如下:
1、指数的定义公式:
对于任意实数a和自然数n,an表示a的n次方,即a的n个相乘。
2、指数幂运算法则:
(a^m)^n=a^(m*n),即两个指数幂相乘,底数不变,指数相乘。a^m*a^n=a^(m+n),即两个指数幂相乘,底数不变,指数相加。(a*b)^n=a^n*b^n,即一个指数幂的积的幂等于每一个底数单独取指数幂后的乘积。a^(-n)=1/(a^n),即一个指数幂的负指数等于底数的倒数取正指数幂。

3、指数函数与对数函数的关系:
ln(a^b)=b*ln(a),即对数函数中对指数函数的运算结果取对数等于指数与对数的乘积。e^ln(a)=a,即指数函数中对对数函数的运算结果取指数等于对数函数的底数。ln(e)=1,即自然对数函数以e为底时,e的对数值为1。
4、指数运算的特殊情况:
a^0=1,任何数的0次方等于1。a^1=a,任何数的1次方等于它本身。0^n=0,0的任何正整数次方都等于0。1^n=1,1的任何次方都等于1。
5、指数函数的性质:
指数函数的图像是一个过点(0,1)且递增的曲线。当指数为正时,指数函数的值逐渐增大;当指数为负时,指数函数的值逐渐减小。指数函数的极限为正无穷大(当x趋近于正无穷)或接近于0(当x趋近于负无穷)。

6、指数运算的推广:
对于实数a和任意有理数r,a^r的运算可以通过把r表示为两个整数的比值,然后将a的这两个指数幂的运算结果进行根号运算来得到。对于实数a和任意实数x,a^x的运算可以通过无限逼近法来计算,即将x表示为无穷小数的形式,然后取有限项的近似值进行计算。
两个数,指数相同底数不同,能让底数直接相乘吗?
底数不同,指数相同的整式乘法算法:a^n×b^n=(a×b)^n。这种运算称为幂运算。底数可以直接相乘,指数不变,计算即可。
运算规则:同底数幂相乘,底数不变,指数相加;同底数幂相除,底数不变,指数相减;幂的乘方,底数不变,指数相乘;同指数幂相乘,指数不变,底数相乘;同指数幂相除,指数不变,底数相除。
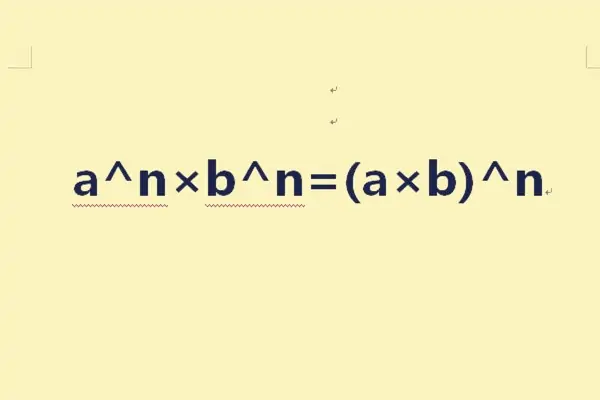
扩展资料:
1、同底数幂的乘法:
aᵐ·aⁿ·aᵖ=aᵐ⁺ⁿ⁺ᵖ(m, n, p都是正整数)。
2、幂的乘方(aᵐ)ⁿ=a(ᵐⁿ),与积的乘方(ab)ⁿ=aⁿbⁿ
3、同底数幂的除法:底数不变,指数相减幂的乘方;
4、幂的指数乘方:等于各因数分别乘方的积商的乘方
5、分式乘方:分子分母分别乘方,指数不变。
同底数幂的除法法则是根据除法是乘法的逆运算归纳总结出来的,和前面讲的幂的运算的三个法则相比,在这里底数a是不能为零的,否则除数为零,除法就没有意义了。又因为在这里没有引入负指数和零指数,所以又规定m>n。能从特殊到一般地归纳出同底数幂的除法法则。
同底数幂的两个幂相除,如果被除式的指数与除式的指数相等,那么商等于1,即am÷an=1,m是任意自然数。a≠0, 即转化成a0=1(a≠0)。
同底数幂的两个幂相除,如果被除式的指数小于除式的指数,即m-n<0时,指数部分为负整数则转化成负整数指数幂,再用负整数指数幂法则。
参考资料来源:百度百科_幂运算







