圆心角和圆周角有什么关系吗?
顶点在圆心上的角叫做圆心角。
圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距也相等。下图的∠AOB就是圆心角。
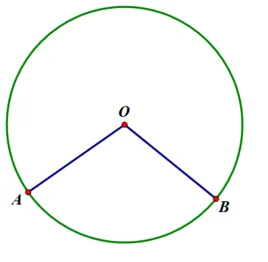
顶点在圆周上的角叫做做圆周角。
圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角都等于这条弧所对的圆心角的一半。下图的∠AOB就是圆周角。
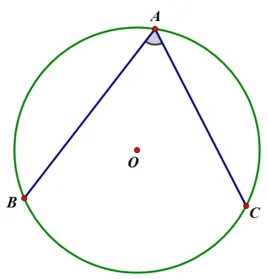
圆心角的度数等于它所对的弧的度数。与弧、弦、弦心距的关系。在同圆或等圆中,若两个圆心角、两条弧、两条弦、两条弦的弦心距中有一组量相等,则对应的其余各组量也相等。
扩展资料:
一条弧的度数等于它所对的圆心角的度数。半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
L(弧长)=(r/180)XπXn(n为圆心角度数,以下同);
S(扇形面积) = (n/360)Xπr2;
扇形圆心角n=(180L)/(πr)(度)。
K=2Rsin(n/2) K=弦长;n=弦所对的圆心角,以度计。
对于一个圆周角,角的内部必然夹了一段圆弧,通常把圆周角说成是这一弧上的圆周角,或说这一弧所对的圆周角。另外,角的外部也有一段圆弧,我们还把圆周角说成是这一弧所含的圆周角。
如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。这两个推论是判定直角或直角三角形的又一依据,为在圆中确定直角,构造垂直关系,创造了条件,因此它是圆中一个很重要的性质。
参考资料来源:百度百科——圆心角
参考资料来源:百度百科——圆周角
圆心角与圆周角的关系是什么?
圆心角:圆心角是指在中心为O的圆中,过弧AB两端的半径构成的∠AOB, 称为弧AB所对的圆心角。圆心角等于同一弧所对的圆周角的二倍。
圆周角:顶点在圆上,并且两边都和圆相交的角叫做圆周角,这一定义实质上反映的是圆周角所具备的两个特征:①顶点在圆上,②两边都和圆相交。这两个条件缺一不可。
圆心角与弧、弦、弦心距的关系:在同圆或等圆中,若两个圆心角、两条弧、两条弦、两条弦的弦心距中有一组量相等,则对应的其余各组量也相等。
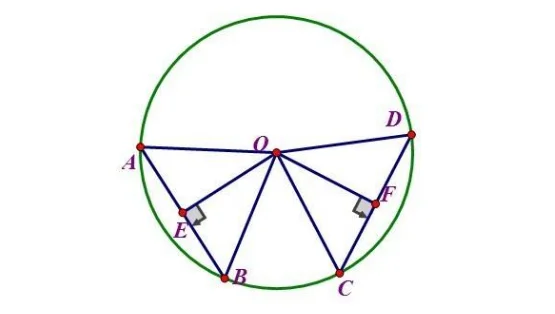
扩展资料
圆心角性质
①顶点是圆心。
②两条边都与圆周相交。
③圆心角性质:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距也相等。在同圆或等圆中,圆心角、圆心角所对的弦、圆心角所对的弧和对应弦的弦心距,四对量中只要有一对相等,其他三对就一定相等。
④一条弧的度数等于它所对的圆心角的度数。
⑤半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径。
参考资料来源:
百度百科—圆心角
百度百科—圆周角
下面分享相关内容的知识扩展:
求圆的周长面积角度公式
、周长公式1、圆的周长 :C=2πr (r:半径)
2、半圆周长:C=πr+2r
二、圆的面积
1、面积:S=πr²
2、半圆面积:S=πr²/2
三、弧长角度公式
1、扇形弧长:L=圆心角(弧度制)×R= nπR/180(θ为圆心角)(R为扇形半径)
2、扇形面积:S=nπ R²/360=LR/2(L为扇形的弧长)
3、圆锥底面半径: r=nR/360(r为底面半径)(n为圆心角)
4、扇形面积公式:S=nπr²/360=rl/2
R:半径,n:弧所对圆心角度数,π:圆周率,L:扇形对应的弧长。
也可以用扇形所在圆的面积除以360再乘以扇形圆心角的角度n。
四、圆的方程:
1、圆的标准方程:在平面直角坐标系中,以点O(a,b)为圆心,以r为半径的圆的标准方程是(x-a)^2+(y-b)^2=r^2。
2、圆的一般方程:把圆的标准方程展开,移项,合并同类项后,可得圆的一般方程是x^2+y^2+Dx+Ey+F=0。和标准方程对比,其实D=-2a,E=-2b,F=a^2+b^2。
五、圆和点的位置关系:
以点P与圆O的为例(设P是一点,则PO是点到圆心的距离),P在⊙O外,PO>r;P在⊙O上,PO=r;P在⊙O内,PO<r.
六、直线与圆有3种位置关系:
无公共点为相离;
有两个公共点为相交;
圆与直线有唯一公共点为相切。这条直线叫做圆的切线,这个唯一的公共点叫做切点.以直线AB与圆O为例(设OP⊥AB于P,则PO是AB到圆心的距离):AB与⊙O相离,PO>r;AB与⊙O相切,PO=r;AB与⊙O相交,PO<r。
拓展资料:
一、圆的性质
(1)圆是轴对称图形,其对称轴是任意一条通过圆心的直线。圆也是中心对称图形,其对称中心是圆心。
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的2条弧。
垂径定理的逆定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的2条弧。
(2)有关圆周角和圆心角的性质和定理
① 在同圆或等圆中,如果两个圆心角,两个圆周角,两组弧,两条弦,两条弦心距中有一组量相等,那么他们所对应的其余各组量都分别相等。
②在同圆或等圆中,相等的弧所对的圆周角等于它所对的圆心角的一半(圆周角与圆心角在弦的同侧)。
直径所对的圆周角是直角。90度的圆周角所对的弦是直径。
圆心角计算公式: θ=(L/2πr)×360°=180°L/πr=L/r(弧度)。
即圆心角的度数等于它所对的弧的度数;圆周角的度数等于它所对的弧的度数的一半。
③ 如果一条弧的长是另一条弧的2倍,那么其所对的圆周角和圆心角是另一条弧的2倍。
(3)有关外接圆和内切圆的性质和定理
①一个三角形有唯一确定的外接圆和内切圆。外接圆圆心是三角形各边垂直平分线的交点,到三角形三个顶点距离相等;
②内切圆的圆心是三角形各内角平分线的交点,到三角形三边距离相等。
③R=2S△÷L(R:内切圆半径,S:三角形面积,L:三角形周长)。
④两相切圆的连心线过切点。(连心线:两个圆心相连的直线)
⑤圆O中的弦PQ的中点M,过点M任作两弦AB,CD,弦AC与BD分别交PQ于X,Y,则M为XY之中点。
(4)如果两圆相交,那么连接两圆圆心的线段(直线也可)垂直平分公共弦。
(5)弦切角的度数等于它所夹的弧的度数的一半。
(6)圆内角的度数等于这个角所对的弧的度数之和的一半。
(7)圆外角的度数等于这个角所截两段弧的度数之差的一半。
(8)周长相等,圆面积比正方形、长方形、三角形的面积大。
参考链接:圆_百度百科
圆锥展开圆心角计算
圆心角公式与母线的关系:圆心角=360度/母线和半径的比值.设扇形半径为r,弧长为L,有这么个规律:圆锥侧面展开的扇形圆心角=r/L *360°
圆心角是指在中心为O的圆中,过弧AB两端的半径构成的∠AOB, 称为弧AB所对的圆心角。圆心角等于同一弧所对的圆周角的二倍。
圆心角的度数等于它所对的弧的度数。
与弧、弦、弦心距的关系:
在同圆或等圆中,若两个圆心角、两条弧、两条弦、两条弦的弦心距中有一组量相等,则对应的其余各组量也相等。
圆周角定理的证明过程
圆周角定理的证明过程如下:

圆周角定理的证明过程:
已知在圆O中,弧AB所对的圆周角为∠ACB,弧AB所对的圆心角为∠AOB。根据圆心角和圆周角的关系,有∠AOB>∠ACB。在优角∠AOB中,取∠AOC=∠ACB,则∠BOC=∠AOB-∠AOC=∠AOB-∠ACB。
根据三角形内角和定理,有∠BOC+∠AOC+∠ACB=180°。所以,∠ACB+∠AOB-∠ACB+∠AOC+∠ACB=180°。即,2∠ACB+∠AOB=180°。因此,圆周角定理得证。
圆周角定理介绍:
圆周角定理指的是一条弧所对的圆周角等于它所对的圆心角的一半。这是圆内最基本和重要的定理之一,是研究圆内其他性质的基础。
具体来说,如果有一条弧AB所对的圆心角为∠AOB,那么圆周角∠ACB等于∠AOB的一半,即∠ACB=1/2∠AOB。这个定理可以通过几何证明或者代数证明。
圆周角定理的意义:
1、证明角相等:
在圆内,可以利用圆周角定理证明两个角相等。例如,在三角形ABC中,BC弧所对的圆周角∠BAC和BC弧所对的圆心角∠BOC相等,因此可以证明∠BAC和∠BOC相等。
2、证明全等三角形:
通过圆周角定理可以证明两个三角形全等。例如,在三角形ABC和三角形DEF中,如果AB弧所对的圆周角∠ACB等于DE弧所对的圆周角∠DFE,那么可以证明三角形ABC和三角形DEF全等。
3、计算角度:
圆周角定理可以用于计算角度。例如,在圆内接四边形ABCD中,如果∠A是直角,那么∠B、∠C、∠D的角度可以通过圆周角定理计算出来。
4、作图:
圆周角定理可以用于作图。例如,在作圆的内接正方形时,可以通过圆周角定理确定四个顶点的位置。证明弧相等:圆周角定理可以用于证明两条弧相等。例如,在圆内接四边形ABCD中,如果AB弧等于CD弧,那么可以证明AB等于CD。







